Parametric Test vs Non-Parametric Test

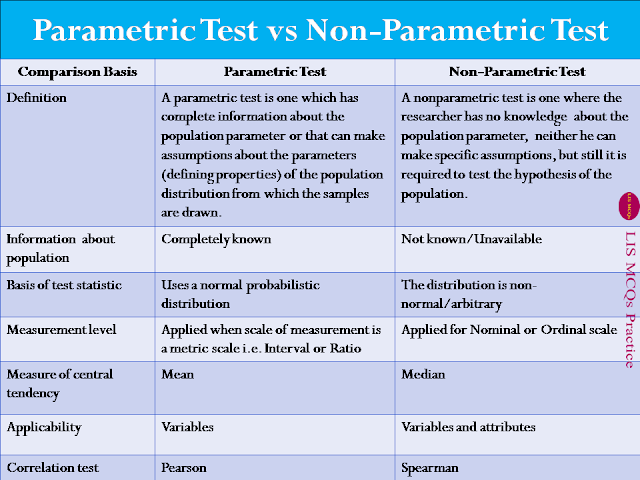
Parametric Test: Parametric tests are those that make assumptions about the parameters (defining properties) of the population distribution from which the sample is drawn. In other words, Parametric tests are used when we have information about the population parameter or at least certain assumptions can be made regarding the characteristics of the population. Examples: t-test, z-test, F-test, ANOVA test, Pearson’s coefficient of correlation.

Non-Parametric Test: Non-parametric tests are normally ‘distribution-free’ and are used for non-normal variables. In contrast to Parametric test, Non-Parametric tests are used when the researcher has no information about the population parameter, neither he can make any assumptions about the population. Examples: Chi-Square Test, Mann-Whitney u-test, Wilcoxon signed-rank test, Wald–Wolfowitz Runs test, Mc-Nemar test, Mood's median test, Spearman correlation coefficient.

PARAMETRIC Vs NON-PARAMETRIC TEST

Parametric tests require assumptions about the distributional characteristics of the population, while Non-parametric tests are distribution free and do not require assumptions so they can be used for non-normal/skewed distributions and where the group variance is not equal.

Parametric tests evaluate hypothesis for a particular parameter, usually the population mean, whereas Non-parametric tests evaluate hypothesis for entire population.

In parametric test, measurement of variables is done on interval or ratio scale. On the other hand, in Non-Parametric test, the variables of interest are calculated on nominal or ordinal scale. Similarly the measure of central tendency in the parametric test is mean, whereas in the case of non-parametric test, measure of central tendency is median.

In the case of parametric test, there is complete information about the population. On the contrary, there is no information about the population distribution in non-parametric test.

Parametric test is applicable for variables only, whereas non-parametric test can be applied for both variables and attributes.

Parametric tests are more powerful than non-parametric tests when the assumptions are correct. However, non-parametric tests are easy to compute especially in the case of non-normal data.

Self-Check Exercises

1.Unlike the non-parametric tests, Parametric test make certain assumptions about __.

(A) the sample size
(B) the population size
(C) the underlying distribution
(D) None of the above

...
Answer: (C) the underlying distribution

2. Which of the following tests is an example of non-parametric method?

(A) t-test
(B) z-test
(C) sign test
(D) All the above

...
Answer: (C) sign test

3. Chi-square test is an example of __.

(A) Parametric test
(B) Non-parametric test
(C) Descriptive test
(D) Survey test

...
Answer: (B) Non-parametric test

4.Which of the following is a non-parametric test?

(A) Analysis of Covariance
(B) Analysis of variance
(C) Median test
(D) Critical Ratio

...
Answer: (C) Median test

5. The Kruskal-Wallis test is the non-parametric alternative to the __.

(A) Factorial design
(B) One-way ANOVA
(C) Two-way ANOVA
(D) None of the above

...
Answer: (B) One-way ANOVA